Context Clustering
You see, that we are talking about phoneme classes like "vowel" or "consonant".
Creating a Question Set
We have not yet defined what a vowel or consonant is. We have to do that now. Start a blank Janus and do:[PhonesSet ps] read ../step2/phonesSetYou have just augmented the PhonesSet object by 11 new phone sets. Now we can easily find out what vowel will mean from now on, the object ps:vowel contains all vowels.
[Tags tags] read ../step2/tags
ps add nonphone +
vowel A AEH AH AI AU E E2 EH ER2 EU I IE J O OE OEH OH U UE UEH UH
consonant B CH D F G H K L M N NG P R S SCH T TS V X Z
sonorant M N R L
nonsonorant B D F G H S
labial B M F
nonlabial D G H L N R S
stop B D G M N
nonstop F H L R S
liquid L R
nonliquid B D F G H M N S ps:phones add @
ps write phonesSet
In the above lines, we've also taken the chance and have added the pad phone such that we don't have to do that every time after we load a PhonesSet from file.
You've see context questions before, in the initCI script. All the questions there started with "0=", which means they were asking questions about the central (or only) phone of a context. Now we want to cluster contexts dependent on the neighboring phones, os we'll need questions that start with "-1=" (left neightbor) or "+1=" (right neighbor). For this we have to build ourselves a QuestionSet object. Why didn't we need one so far, although we were obviously working with questions before. That's because the Tree object that uses question has an internal QuestionSet object, that it creates and fills automatically. Now we have developed new questions, that don't occur anywhere else, and we want to limit the usage of decistion tree questions to the phone sets we've just defined. So here we go:
QuestionSet qs ps:PHONES ps tagsSo we have now produced a question set that contains questions about the right or the left neighbor belonging to one of the previously defined sets, and the same questions with additionaly asking for the word boundary flag on either side. Also we have added questions about the word boundary flag alone. The question "0=WB" means "is the current phone a word-boundary phone?", and "0=WB +1=WB" means "are both, the current phone and its right neighbor word boundary phones?"
qs add "0=WB"
qs add "0=WB +1=WB"
qs add "0=WB -1=WB"
qs add "0=WB -1=WB +1=WB"
foreach p [ps:] {
qs add "+1=\$p" ; qs add "+1=\$p +1=WB"
qs add "-1=\$p" ; qs add "-1=\$p -1=WB"
}
qs write questionSet
Running the Clustering Algorithm
The complete algorithm can be found in the script thread.The startup is the same as for training the context dependent models. After the starup we should not forget to configure the pad phone, for both the distribution tree and the question set, load the distribution weights and define a minimal frame count we will want to have eventually per polyphone cluster:
qs configure -padPhone padThe distribution tree object offers a method split which will take a tree node, put a given question in it, and creates three successor nodes, one for each of the possible answers "no", "yes", "don't know". Since we are using a pad phone, the don't-know-nodes will never be used. The ptree that is attached to a node which is being split will also be split. Every new successor node will get its own ptree containing only the polyphones that belong to them.
dst configure -padPhone pad
dss load ../step11/distribWeights.2
dss configure -minCount 250
The main clustering loop works on a sorted list of possible splits. It will always perform the split that gives the best score. Once a split is performed, it is taken out of the list, and the possible splits for the new successors are inserted into the list which is kept sorted such that the first element of the list is always the best split.
Initially we don't have anything in our list, but we have 32 nodes in our tree that have ptrees attached and could be split. So the first thing we do is create a list of all possible splits for all ptree-carrying nodes:
foreach node [dst:] { findQuestion dst \$node qs \$node nodes count }
set scores [lsort -real -decreasing [array names nodes]]
Here we assume the existence of a procedure "findQuestion" which finds the best scoring questing out of a given set qs of questions for a given node \$node of a given distribution tree dst, adding the node and the found question - if applicable - to the list nodes(x), where x is the score of the found question. "Applicable" means, that nothing will happen, if no question can be found because of too low counts or other constraints. The count variable will always contain the number of so far added succesor nodes to the original distribution tree node. The above "lsort" line is doing the mentioned sorting. It fills the list scores with all so far found scores. So [lindex \$scores \$n] would give us the n-best score, and \$node([lindex \$scores \$n]) would give us a list of all splits that would get that score. Usually scores are floating point numbers such that the case that two splits get the same score happens very rarely.
Equipped with such a procedure we can now write the following loop:
while { [llength \$scores] } {
set score [lindex \$scores 0]
set nlist \$nodes(\$score)
unset nodes([lindex \$scores 0])
foreach node \$nlist {
set name [lindex \$node 0]
set par [lindex \$node 1]
set quest [lindex \$node 2]
if { [string length \$quest] } {
set c \$count(\$par)
puts "\$name \$quest (\$score) \${par}(\$c) -> ([expr \$c+1]) ([expr \$c+2])"
dst split \$name \$quest \${par}(\$c) \${par}([expr \$c+1]) \${par}([expr \$c+2])
incr count(\$par) 3
for {} { \$c < \$count(\$par)} { incr c} {
if { [set idx [dst index \${par}(\$c)]] > -1} {
findQuestion dst \${par}(\$c) qs \$par nodes count
}
}
}
}
if [array exists nodes] {
set scores [lsort -real -decreasing [array names nodes]]
} else { set scores {}}
}
In this loop we stay as long as there are splits available in the nodes array, i.e. as long as the scores list is not empty. In the first three lines of the loop we extract the splits that have the best score, and remove them from the nodes array. Then for each of the best scoring splits we extract the nodename to be split ($name), the name of the orignal distribution tree node (\$par), and the splitting question ($quest). The the split method creates three nodes which have the name of the orignal node plus a suffix which is (\$c), (\$c+1), or (\$s+2). The successor count of the orignal node is increased by three, and eventually we call the findQuestion procedure again for all new nodes that resulted from the split.
Now it's time to talk about the "findQuestion" procedure, which, of course, must be defined before the above discussed loop. Well, here it comes:
proc findQuestion { tree node qs parent nodesA countA } {
upvar \$countA count
upvar \$nodesA nodes
if { [set p [\$tree:\$node configure -ptree]] >= 0} {
set c [\$tree.ptreeSet.item(\$p) configure -count]
set question [\$tree question \$node -questionSet \$qs]
set score [lindex \$question 1]
set question [lindex \$question 0]
if { [string length \$question] } {
lappend nodes(\$score) [list \$node \$parent \$question \$c]
if {! [info exist count(\$parent)]} {set count(\$parent) 0}
}
}
}
The procedure first checks if there is a ptree attached to the given node. Only if there is a ptree attached, the "question" method of the tree object is called. This hard coded Janus-internal function will return the one best scoring question from the given question set that would split the given node. If no question was found (e.g. because the resulting successors frame-counts would become too small, or because every available question would have a constant answer for all polyphones in the ptree) then nothing happens, otherwise the description of the found split is added to the nodes array, which contains all splits of the same score.
When all the splitting is done, no more nodes can be split, then the loop ends and we can save the current status for later use:
dst write distribTreeClustered
dst.ptreeSet write ptreeSetClustered
Adding Context-Dependent Codebooks
Now we have a tree that looks something like this:
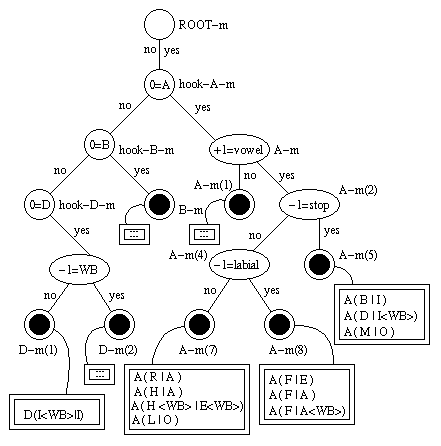
The dotted circles are leaf nodes of the distribution tree, the double-edged boxes are PTrees, four of which are show in detail. You can see e.g. that the PTree that is attached to node A-m(9) contains only polyphones whose left context (i.e. context -1) is F. This is so, because F is the only phone that does not belong to the "stop" phone set but belongs to the "labial" phone set.
In our current system we have a distribution for every single polyphone, and only 34 codebooks. What we would like to have now, is an extra codebook for each of the leaf nodes of the distribution tree, these are the nodes that have ptrees attached. These new codebooks will also need their mixture weights distributions. So what we are going to do is add codebooks to cbs and add distributions to dss for every node of dst that holds a non-empty ptree. Here it is:
set itemN [dst configure -itemN]The for loop loops over all items (i.e. nodes) of the distribution tree. It checks if the current node has a ptree attached, and only if it has one it gets the nodes name, and all the distribution indices that were assigned to the polyphones in the attached ptree. The PTree object's method "models" does write all distribution indices in a ModelArray object.
for { set i 0} { \$i < \$itemN} { incr i} {
if { [set ptree [dst.item(\$i) configure -ptree]] > -1} {
set node [dst.item(\$i) configure -name]
dst.ptreeSet.item(\$ptree) models [ModelArray dtabMA dss]
if { [llength [set models [dtabMA puts]]] } {
cbs add \$node LDA 16 12 DIAGONAL
cbs:\$node := cbs.item([dss:[lindex [lindex \$models 0] 0] configure -cbX])
set cbX [cbs index \$node]
foreach ds \$models { dss:[lindex \$ds 0] configure -cbX \$cbX }
if { [dst.item(\$i) configure -model] < 0 } {
dss add \$node \$node
dst.item(\$i) configure -model [dss index \$node]
}
}
dtabMA destroy
}
}
Then, if this model array in not empty (could be the case for initially created ptrees that have never got any polyphone), we add a new codebook with the same name as the dst-node to the codebook set, initialize its parameters with the from the codebook that was used for any one of the distributions in the models array (should be the same for all), and then make all distributions in the models array use the newly created codebook. Also we add a new distribution with the same name as the codebook and tell the leaf node of the distribution tree to now use this newly created distribution.
Eventually we write out the finished clustered codebook and distribution description files.:
cbs write codebookSetClustered
dss write distribSetClustered
Pruning The Distribution Tree
So far we still have all the ptrees attached to the distribution tree, also we stell have lots of distributions in the distribution set. If we want to continue with the clustered acoustic models only, and are not interested in the single polyphones any more, we should simple prune them away from the tree, and create a distribution set, that contains only the distributions that we really need:[DistribSet dss2 cbs]We call the new distribution set dss2, and, in a loop over all nodes of the distribution tree, we add a distribution for each node that has been assigned a model. In the same loop we detach all attached ptrees that we find.
foreach node [dst:] {
set model [dst:\$node configure -model]
set ptree [dst:\$node configure -ptree]
if { \$ptree > -1 } { dst:\$node configure -ptree -1 }
if { \$model > -1 } {
set dsname [dss name \$model]
dss2 add \$dsname [cbs name [dss:\$dsname configure -cbX]]
}
}
Eventually we write the description of the now clustered and pruned distribution set and distribution tree:
dst write distribTreeClusteredPruned
dss2 write distribSetClusteredPruned